Solutions to exercises
Source: Gray (2004) . Sec. 3.18, p. 54-55.
Exercise 54:
a)
c=1−p
b)
P{W=0}=∑k=0∞P{W=0∣N=k}P{N=k}=(1−p)∑k=0∞(2p)k=1−p/21−pP{W=1}=2−pp
c)
P{N=k∣N<10}=⎣⎢⎡1−p101−ppk,0,0≤k<10k≥10
Exercise 55:
a)
PYn(k)=[(1−p)(1−ϵ)+pϵp(1−ϵ)+(1−p)ϵk=0,k=1
b)
Yes, it is a Bernoulli process.
c)
PYn∣Xn(j∣k)=⎣⎢⎢⎢⎡1−ϵϵϵ1−ϵj=0,k=0,j=1,k=0j=0,k=1j=1,k=1
d)
PXn∣Yn(j∣k)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡(1−p)(1−ϵ)+pϵ(1−p)(1−ϵ)(1−p)(1−ϵ)+pϵpϵp(1−ϵ)+(1−p)ϵ(1−p)ϵp(1−ϵ)+(1−p)ϵp(1−ϵ)j=0,k=0,j=1,k=0j=0,k=1j=1,k=1
e)
P{Yn=Xn}=P{Wn=1}=ϵ
Source: Beichelt, F. (2016). (Chapter 8, p. 376 and Chapter 10, p. 492)
Exercise 8.1:
(1)
P{X2=2∣X1=0,X0=1}=P{X2=2∣X1=0}=p02=0.5
P{X2=2,X1=0∣X0=1}=P{X2=2∣X1=0,X0=1}P{X1=0∣X0=1}=p02p10=0.2
(2)
P{Xn+1=2,Xn=0∣Xn−1=0}=P{X2=2,X1=0∣X0=0}=p02p00=0.25
(3)
P{X1=2}=0.4p02+0.3p12+0.3p22=0.5P{X1=1,X2=2}=p12P{X1=1}=0.4(0.4p01+0.3p11+0.3p21)=0.072
Exercise 8.2:
(1)
P(2)=P2=⎝⎜⎛0.580.320.360.120.280.180.30.40.46⎠⎟⎞
(2)
P{X2=0}=0.42
P{X0=0,X1=1,X2=2}=P{X0=0}⋅p01⋅p12=0
Exercise 8.3:
(1)
P{X3=2}=(0,0,1)(P3)⊺(0.4,0.4,0.2)⊺=0.2864
(2)
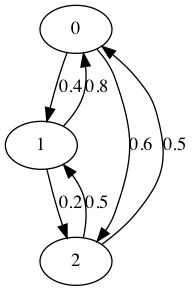
(3)
π=⎝⎜⎛0.39470.30700.2982⎠⎟⎞
Exercise 8.4:
It is not a Markov process. For instance:
pX3∣X2,X1(1∣0,1)=0
but
pX3∣X2(1∣0)=41
Exercise 8.5:
(1)
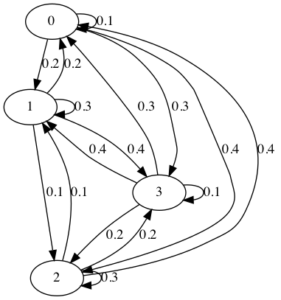
(2)
π=⎝⎜⎜⎜⎛0.250.250.250.25⎠⎟⎟⎟⎞
Exercise 10.1
(1)
E{Xn+1∣X0,…,Xn}=E{Yn+12+Xn∣X0,…,Xn}=E{Yn+12}+Xn>Xn⇒
It is not a martingale. It is a submartingale.
(2)
E{Xn+1∣X0,…,Xn}=E{Yn+13}+Xn=Xn⇒
It is a martingale.
(3)
E{Xn+1∣X0,…,Xn}=E{∣Yn+1∣}+Xn>Xn⇒
It is a submartingale.
Exercise 10.2
E{Xn+1∣X0,…,Xn}=E{Yn+1−E{Yn+1}}+Xn=Xn⇒
It is a martingale.
Ex. 10.3
E{Xn+1∣X0,…,Xn}=2TXn⇒
- It is a martingale for T=2.
- It is a submartingale for T≥2.
- It is a supermartingale for 0<T≤2.
Ex. 10.4
E{XN−1}=−∞
Ex. 10.6
(1)
The winnings after losing 5 games and winning the 6th one are € 122
(2)
Yes, it is a martingale
Ibe, 2013, Pages 29-48
Ex. 2.12:
(a) For
p=21
it is a martingale.
(b) For
p≥21
it is a submartingale
(c) For
p≤21
it is a supermartingale
Ex. 2.13.
TBD
Ex. 2.14.

